대학 수업 정리/수학1
대학수학1 6장 역함수(Inverse Functions)
민경현(Kyunghyun Min)
2020. 7. 4. 22:50
역삼각함수, 쌍곡함수, 부정형, 로피탈 법칙에 대해 정리합니다.
6.6. Inverse Trigonometric Function(역삼각함수)
일대일 함수를 만들기 위해서 범위를 제한한다.
- arcsin x 또는 sin-1 x
- arccos x 또는 cos-1 x
- arctan x 또는 tan-1 x
domain(정의역) rage(치역) horizontal asymptote(수직 점근선)
6.6.1.역함수 구간

6.6.2. 미분
증명은 음함수 미분으로 한다.
tan-1x의 미분은 모르면 적분 못 한다.

6.7. Hyperbolic Function (쌍곡선 함수)
sinh x = (ex - e-x) / 2
cosh x = (ex + e-x) / 2
tanh x = sinh x /cosh x
미분
(cosh x)' = sinh x
(sinh x)' = cosh x
(tan x)' = 1/(coshx)2
참고)
cosh(x) = cos(xi)
sinh(x) = - i sin(xi)
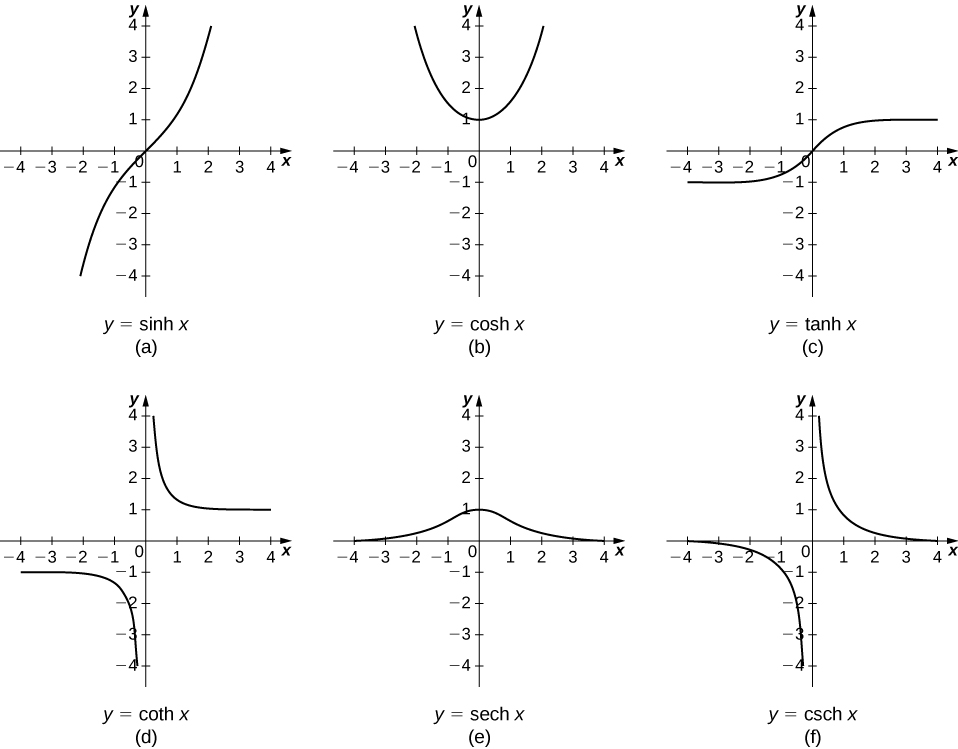
삼각함수의 성질과 거의 비슷하다.
6.8. Indeterminate Forms(부정형)
극한 & 미분 가능을 응용한다.
6.8.1. 7가지 부정형
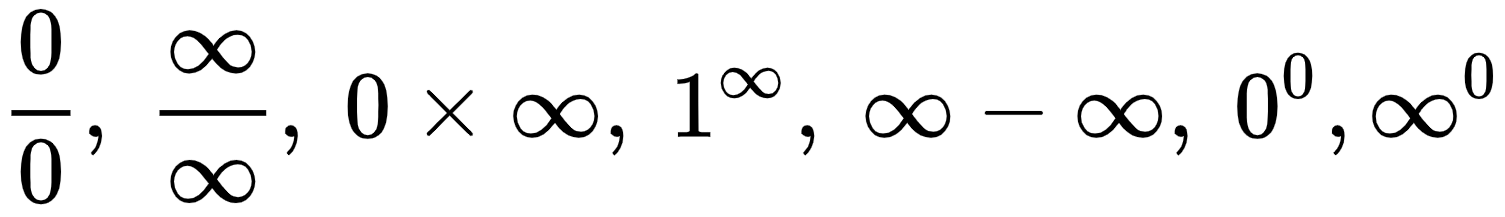
⇒ 결국 모두 0/0꼴로 바꾸어 로피탈 정리(미분의 정의)를 사용
주의 ) 0∞ 꼴 = 0 부정형 아님
6.8.2. L'Hospital's Rule(로피탈 법칙)
로피탈 법칙은 0/0 꼴과 ∞ / ∞꼴 에 대해서만 정의 되어 있다.
증명
미분 정의 사용
로피탈 정리를 사용 표기법
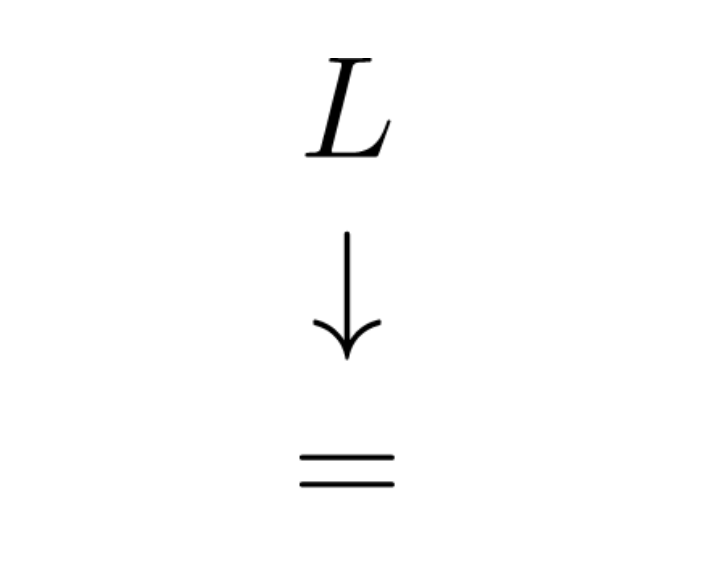
6.8.3. 0 / 0 꼴
f,g 미분가능, limx→af(x)=0, limx→ag(x)=0, y = f/g →
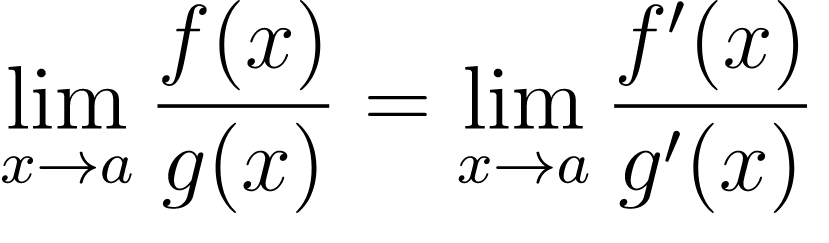
6.8.4. ∞ / ∞꼴
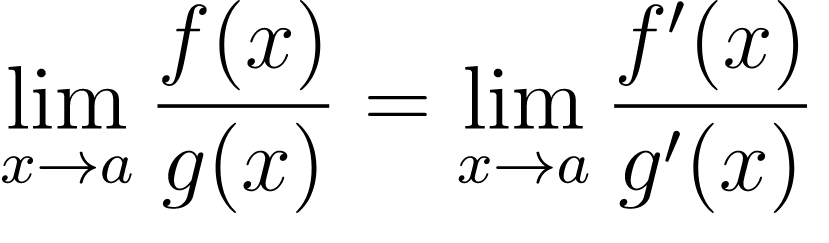
방법
0/0꼴로 바꾸어 증명
lim f/g = lim (1/f) / (1/g)
ln(x), x , ex 속도 비교
limx→1ln(x) / (x-1) = lim 1/x = 1 // 의미: 증가 속도 같은 근사로 볼 수 있다.
limx→∞ex/x2 = lim ex/2x = lim ex/2 = ∞
6.8.5. 0 x ∞ 꼴
방법
f * g = f / (1/g)
0/0꼴 또는 무한대/무한대 꼴로 만들어 로피탈 법칙 사용
주의
미분 쉽게 되도록 바꾸기
6.8.6. ∞ - ∞ 꼴
직감 필요
6.8.7. Indeterminate Powers
00 꼴 // ∞0 꼴 // 1∞ 꼴
방법
식에 로그 취하여 지수를 곱하기 꼴로 바꾸기
ln(y) = g(x) * ln(f(x))
[f(x)]g(x) = exp( g(x) * ln (f(x)) )
g(x) * ln (f(x)) ⇒ 0x∞ 꼴